| Numero di pattini per guida |
Fattore di contatto |
1 |
1 |
| 2 |
0,81 |
| 3 |
0,72 |
| 4 |
0,66 |
| 5 |
0,61 |
| Urti e vibraz. |
Velocità (V) |
Valore di vibrazione ( G ) |
Fw |
| Senza urti o vibr. |
A basse velocità V≤15 m/min |
G <= 0,5 |
1 ~ 1,5 |
| Senza sign. urti o vibraz. |
A medie velocità 15<V≤60 m/min |
0,5 < G <= 1,0 |
1,5 ~ 2,0 |
| Con urti o vibraz. |
Ad alte velocità V > 60 m/min |
1,0 < G <= 2,0 |
2,0 ~ 3,5 |
|
Il carico dinamico C è inteso come il carico con il quale si ha una durata nominale di 50 Km di distanza percorsa mantenendo invariato il carico applicato in entità e direzione. Ciò è valido per un sistema lineare a sfere.
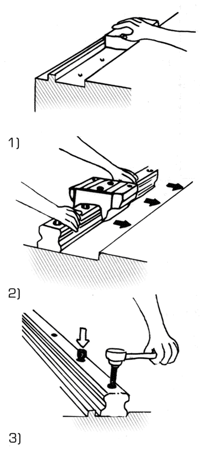
Quando il sistema lineare, in movimento o fermo, è sottoposto a carichi eccessivi o a grossi urti, questi provocano una deformazione permanente locale tra la pista di scorrimento e gli elementi volventi. Se la deformazione è eccessiva, ne viene compromessa la scorrevolezza del sistema lineare.
Definiamo la capacità di carico statico ammissibile C0 come il carico statico di grandezza e direzione costanti che genera, nel punto di massima sollecitazione tra le parti in contatto, una deformazione totale permanente di 0,0001 volte il diametro dell'elemento volvente.
Quando il sistema lineare è soggetto a dei movimenti, gli elementi volventi hanno il loro massimo stress ad entrambe le estremità.
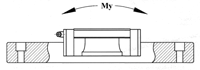
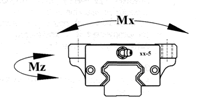
Definiamo il momento statico ammissibile M0 come il momento statico di grandezza e direzione costanti che genera, nel punto di massima sollecitazione tra le parti di contatto, una deformazione totale permanenete di 0,0001 volte il diametro dell'elemento volvente.
Il momento statico ammissibile di un sistema lineare è definito per le tre direzioni MX, MY e MZ.
Il fattore di sicurezza statico fs è il rapporto tra la capacità di carico statico e il carico agente sul sistema lineare.
Nei sistemi con moto lineare, è difficile ottenere una distribuzione uniforme del carico per l'influenza di diversi fattori quali la precisione delle lavorazioni delle superfici di appoggio delle guide nonché del montaggio delle stesse. Quando due o più pattini sono montati sulla stessa guida, si dovrà moltiplicare le capacita di carico dinamico e statico (C e CO) per i fattori di contatto fc indicati in tabella.
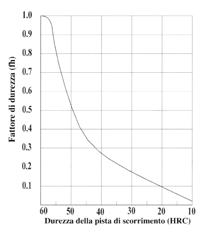
La migliore capacità di carico ammissibile per un sistema lineare si ottiene con una durezza di HrC 58-64 sulle piste di rotolamento. Se tale durezza e inferiore a HrC 58, sia la capacità di carico statica CO che la capacità di carico dinamica C dovranno essere moltiplicati per il fattore di durezza fh.
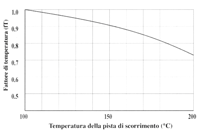
Quando la temperatura di un sistema lineare supera i 100 ° C, diminuisce la durezza delle piste di rotolamento e quindi la durata del sistema risulta essere più breve. Si dovrà perciò tener conto del fattore di temperatura ft nel calcolo della durata nominale.
Nota 1: per temperature elevate dovranno essere considerate le dilatazioni dei materiali.
Fattore di carico Fw
Normalmente, il movimento alternative delle macchine utensili e non, comporta vibrazioni ed urti. Le vibrazioni sono dovute alle alte velocità mentre gli urti ai continui avvii ed arresti degli assi. Quando questi fattori influenzano significativamente i carichi effettivi, si dovrà dividere le capacità di carico dinamico C e statico CO con i fattori di carico empirici sotto riportati.
Calcolo della durata nominale L
La durata nominale rappresenta la distanza totale che viene superata praticamente con una probabilità del 90% senza nessuno sfaldamento delle piste di scorrimento di un gruppo degli stessi sistemi lineari funzionanti indivi-dualmente nelle stesse condizioni di lavoro. La seguente formula esprime la durata nominale di un sistema lineare a sfere conoscendo la capacita di carico dinamico C ed il carico applicato P: L = ((fh x fT x fc/fw) x (C/P))³X 50 (km)
L : durata nominale fh: fattore di durezza
C : capacita di carico dinamico
P : carico applicato
fT: fattore di temperatura
fc : fattore di contatto
fw : fattore di carico
Calcolo della durata di servizio in ore
Quando i valori della lunghezza della corsa ed il numero dei cicli alternativi sono costanti, si utilizza la seguente formula:
Lh = Lx 10 3 (h )
2 x Is x nl x 60
Lh : durata di servizio in ore (h)
L : durata nominale (km)
Is : lunghezza della corsa (m)
nl : numero dei cicli alternativi al minuto |
|
|
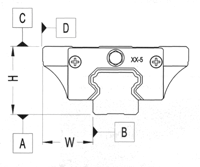
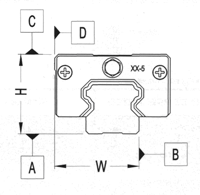
| CLASSE DI PRECISION E |
(H) |
(P) |
(S) |
| Tolleranza della quota H |
± 0,04 |
0 / - 0,04 |
0 / - 0,02 |
| Tolleranza della quota W |
± 0,04 |
0 / - 0,04 |
0 /- 0,02 |
| Differenza della quota H tra due pattini di una stessa guida (ΔH) |
0,02 |
0.01 |
0,005 |
| Differenza della quota W tra due pattini di una stessa guida (ΔW) |
0,02 |
0.01 |
0,005 |
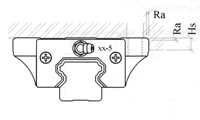
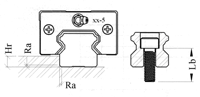
| Parallelismo sulla lunghezza tra la superficie C e la superficie A |
ΔC vedere grafico
|
| Parallelismo sulla lunghezza tra la superficie D e la superficie B |
ΔD vedere grafico |
|
unità di misura: mm
Valori di parallelismo considerando la lunghezza e la precisione della guida. |
| Tipo di precarico |
Simbolo |
Valore di precarico |
| Nessun precarico |
Z0 |
0 |
| Precarico leggero |
Z1 |
0,02 C |
| Precarico medio |
Z2 |
0,05 C |
| Precarico elevato |
Z3 |
0,07 C |
|
| C: valore di carico dinamico |
|